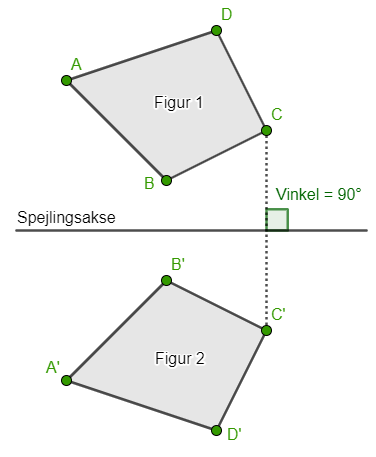
Figurer kan spejles i en linje som kaldes en spejlingsakse. Når en figur spejles i en spejlingsakse, er den spejlede figur konkgruent med den orginale figur

Figur 1 spejles i spejlingsaksen over i figur 2.

Afstanden fra punkterne til spejlingsaksen er den samme på begge sider af spejlingsaksen.

Punkterne spejles vinkelret på spejlingsaksen.

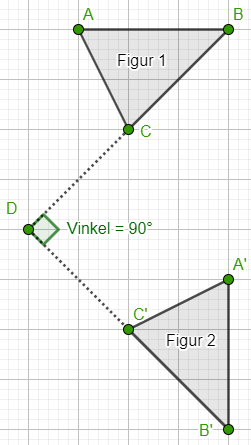
En drejning af en figur foretages ved at dreje alle figurens hjørnepunkter omkring det samme punkt.

Punktet der drejes omkring kaldes drejningspunktet.

Alle punkter drejes det samme antal grader rundt om drejningspunktet med eller imod urets retning.

Figur 1 drejes om punktet D i 90° med urets retning. På den måde opstår figur 2

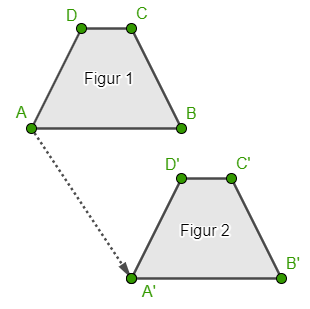
Ved en parallelforskydning flyttes figuren i en bestemt retning og i en bestemt afstand

Figur 1 er parallelforskudt i pilens retning

Figur 1 og figur 2 er konkgruente altså helt ens

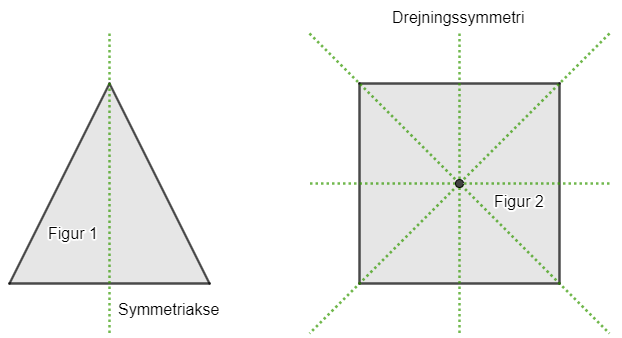
En symmetriakse er en linje der ligger inde i en figur og deler figuren i 2 identiske figurer som spejles over i hinanden

Figur 1 har en symmetriakse

Figur 2 har 4 symmetriakser

Figur 2 har også drejningssymmetri, da figuren kan drejes mindre end 360° om et punkt, så figuren ligger oven i sig selv igen

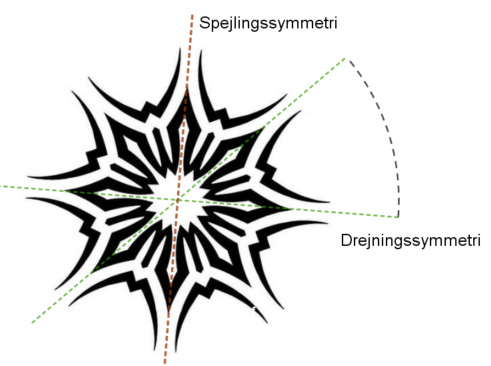
Et rosettemønster indeholder en grundfigur som ved hjælp af dregning danner et mønster

Et rosettemønster kan også indeholde en spejlingssymmetri

Figuren til højre har en både spejlingssymmetri og drejningssymmetri

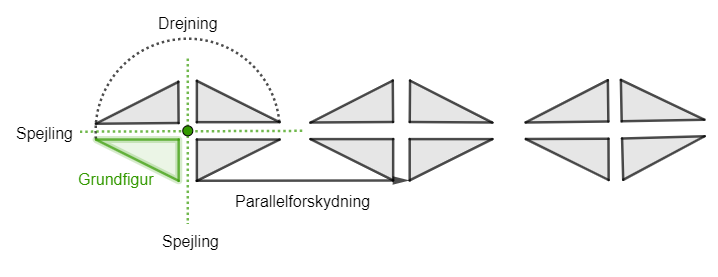
En frise er et mønster der gentager sig selv

En frise indeholder en grundfigur som ved hjælp af drejning, spejling eller parallelforskydning, danner et mønster

Figuren til højre har en trekant som grundfigur. Ved hjælp af spejling, drejning og parallelforskydning fremkommer et mønster som kaldes en frise

En tesselation består af geometriske figurer som tilsammen kan dække en hel flade

På billedet til højre ses forskellige grundfigurer, som er sat sammen til et mønster, som kan dække en hel flade

En tesselation kan også bestå af en grundfigur som ved hjælp af flytninger kan dække en hel flade.