Funktioner
Lineær funktion
|
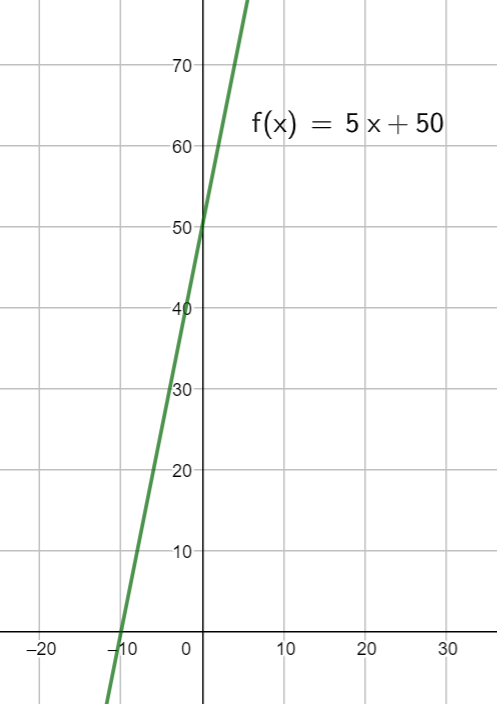
"En lineær funktion er bygget op om forskriften y = ax + b."
a - kaldes for hældningstallet eller hældningskoefficienten b - er et udtyk for hvor funktionen skærer y aksen. b er en konstant mens a er en variabel. Et eksempel kunne være. En taxatur koster 50kr. i startgebyr og 5kr. pr km du kører. |
|
Ligefrem proportionalitet
|
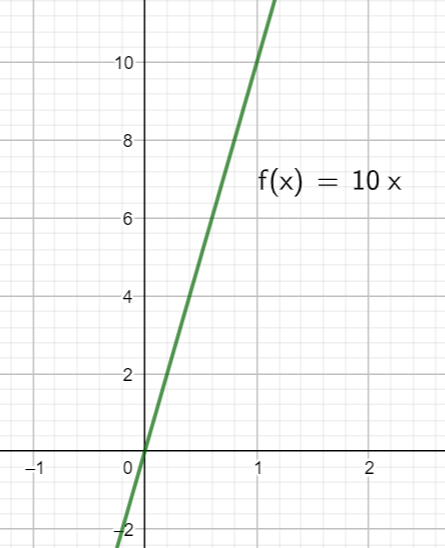
"Når du har 2 variable eksempelvis en x og en y og hvis du ganger x værdien med en kontant og resultatet er y, er der tale om en ligefrem proportionalitet. Ligefrem proportionalitet kan tegnes som en ret linie i et koordinatsystem"
Et eksempel kunne være et besøg i en forlystelsespark hvor du betaler 10kr. for hver forlystelse du prøver. |
|
Stykvis lineær funktion
|
"En Stykkevis lineær funktion har den samme forskrift, som den almindelige lineær funktion nemlig f(x)=ax+b. En stykkevis lineær funktion er en kurve i et koordinatsystem, som består af stykker der hver for sig er en lineær funktion"
Et eksempel kunne være et mobilabonnement hvor du betaler en fast pris på 50kr. for 100 sms'er, derefter skal du betale 2 kr. pr sms. |
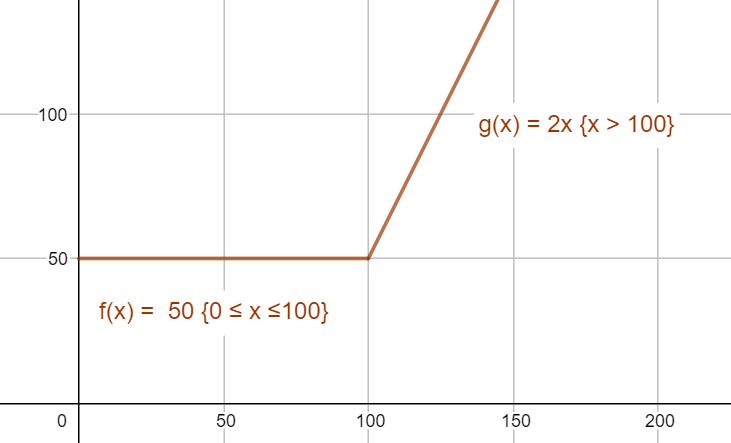
|
Andengradsfunktion
|
"En andengradsfunktion er en funktion, hvor x værdien bliver ganget med sig selv. Linjen for en andengradsfunktion kaldes for en parabel. Forskriften for en andengradsfunktion skrives:"
f(x) = ax2 + bx + cTil højre herfor er tegnet en parabel af en andengradsfunktion |
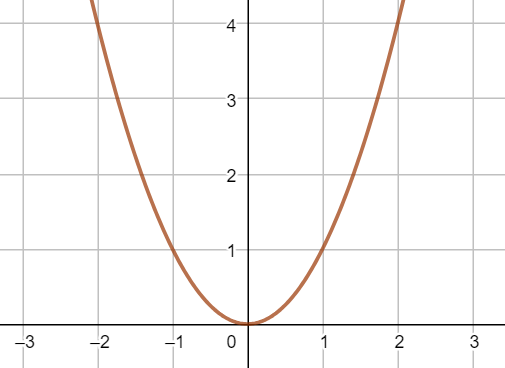
|
Omvendt proportionalitet
|
"Omvendt proportionalitet, betyder at hvis x værdien bliver fordoblet bliver y værdien halveret. Linjen for omvendt proportionalitet kaldes for en hyperbel. Forskriften for omvendt proportionalitet skrives:"
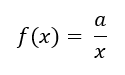
Til højre herfor er tegnet en hyperbel |
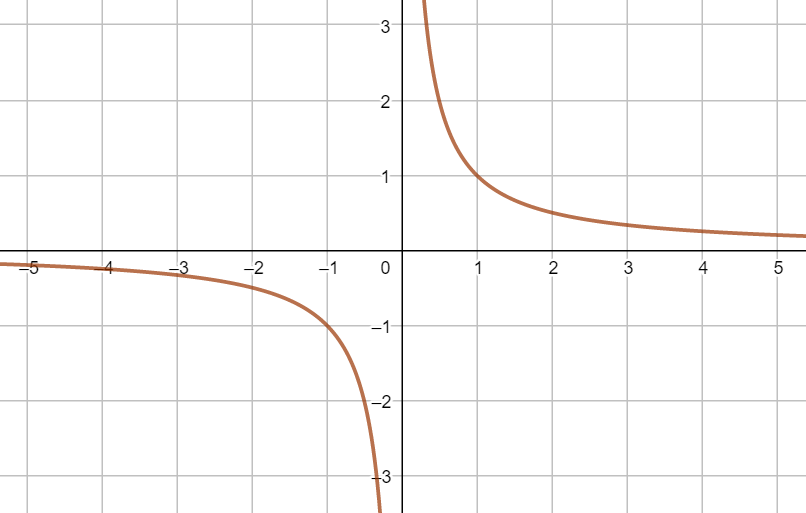
|
Eksponentiel funktion
|
"Den eksponentielle vækst er en måde, hvorpå en mængde kan forøges eller formindskes. Dette er f.eks. formeringen af bakterier eller henfald af radioaktive stoffer. Renters rente er også et eksempel på en eksponentiel vækst"
f(x) = b • axTil højre herfor er tegnet et eksempel på en eksponentiel funktion |
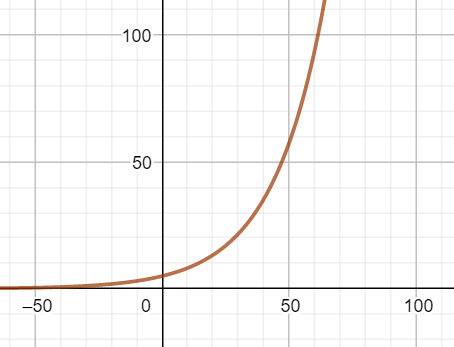
|
© 2019 All Rights Reserved. Læs om privatvilkår