Sandsynlighed
Sandsynlighed
|
"Sandsynlighed skrives som et tal mellem 0 og 1. Sandsynlighed skrives ofte som en brøk, procent eller som decimaltal. Sandsynligheden for at slå en 6'er med en 6-sidet terning er: 1/6 eller som 16,66%" |
Udfaldsrum
|
"Et udfaldsrum er det resultat, man får fra et eksperiment. For eksempel, hvis man kaster en 6-sidet terning, kan udfaldene være 1, 2, 3, 4, 5, eller 6." |

"Udfaldsrummet er: 1, 2, 3, 4, 5, 6" |
Hændelse
|
"En hændelse er et sæt af mulige udfald fra et eksperiment eller en tilfældig proces. En hændelse kan bestå af et enkelt udfald eller flere udfald."
Typer af hændelser: 1) Enkelt hændelse "En enkelt hændelse, er en hændelse der består af præcis ét udfald. For eksempel er hændelsen "at slå en 3'er med en terning" en enkelt hændelse" 2) Sammensat hændelse "En sammensat hændelse, består af flere mulige udfald. For eksempel er hændelsen "at slå et lige tal med en terning" en sammensat hændelse, da udfaldene er: 2, 4, og 6." 3) Sikker hændelse "En sikker hændelse, er en hændelse der altid vil indtræffe. For eksempel er hændelsen "at slå et tal mellem 1 og 6 med en 6-sidet terning" en sikker hændelse." 4) Umulig hændelse "En umulig hændelse, er en hændelse der aldrig vil indtræffe. For eksempel er hændelsen "at slå en 7'er med en 6-sidet terning" en umulig hændelse." |
Udregning af sandsynlighed
|
"Du kan regne på hvad sandsynligheden er for at hændelse vil ske. Det hedder teoretisk sandsynlighed"
Eksempel på en opgave: "Hvad er sandsynligheden for at slå en 6'er med en 6-sidet terning?" 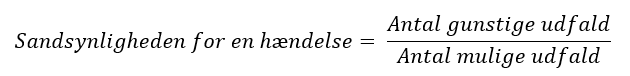
Udfaldsrummet er: 1, 2, 3, 4, 5, 6 Antal mulige udfald er derfor 6, da udfaldsrummet indeholder 6 tal Hændelsen er: 6 Antal gunstige udfald er derfor 1, da hændelsen indeholder et tal |
Udregning: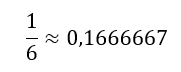
Resultatet kan skrives på 3 måder: 16,67% 1/6 0,1667 |
Tælletræ
|
"Et tælletræ er en måde at synligggøre et udfaldsrum på. Det kan også vise en mulig hændelse udfra et tælletræ
Tælletræet herunder viser de forskellige muligheder når du slår med en 6-sidet terning to gange i træk" 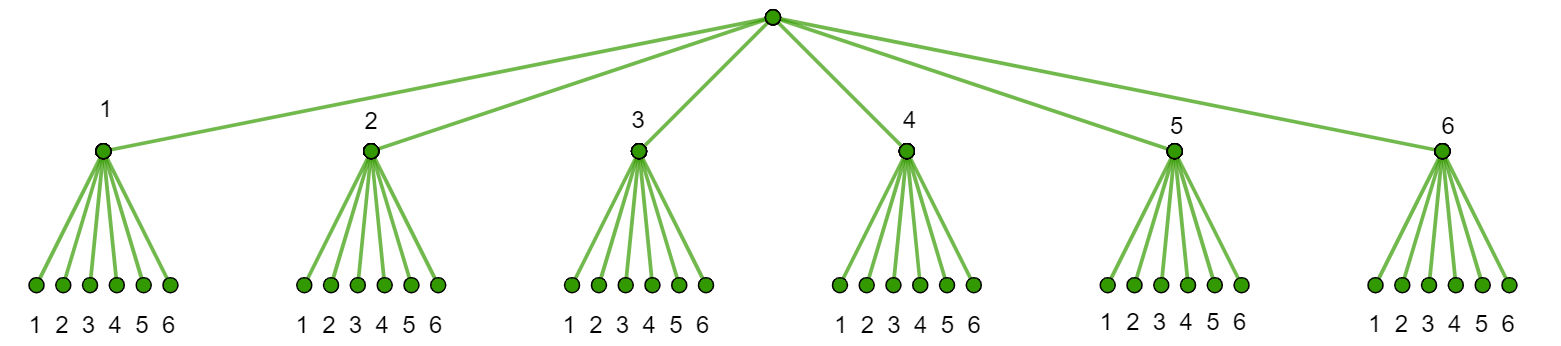
|
Både- og (Gange)
|
"Både- og princippet skal du bruge når der er flere krav til flere hændelser efterfulgt af hinanden. Hvis der i en opgave er flere krav, skal du lægge mærke til om alle krav skal være opfyldt" Eksempel på en opgave "Du skal slå to gange med en 6-sidet terning. Udregn sandsynligheden for at du slår en 5 både første gang og anden gang." Det vigtige er at lægge mærke til, at begge krav i opgaven skal være opfyldt. Begge gange du slår skal du slå en 5'er. Når alle krav skal være opfyldt, skal du gange alle sandsynlighederne sammen, for at finde resultatet. Udregning For hver gang du slår med terningen er der 1/6 sandsynlighed for at slå en 5'er 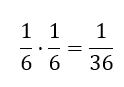
Tælletræet herunder viser mulighederne når du slår med en 6-sidet terning to gange Den røde streg viser der er 1 mulighed ud af 36 muligheder for at slå en 5'er første gang og anden gang" 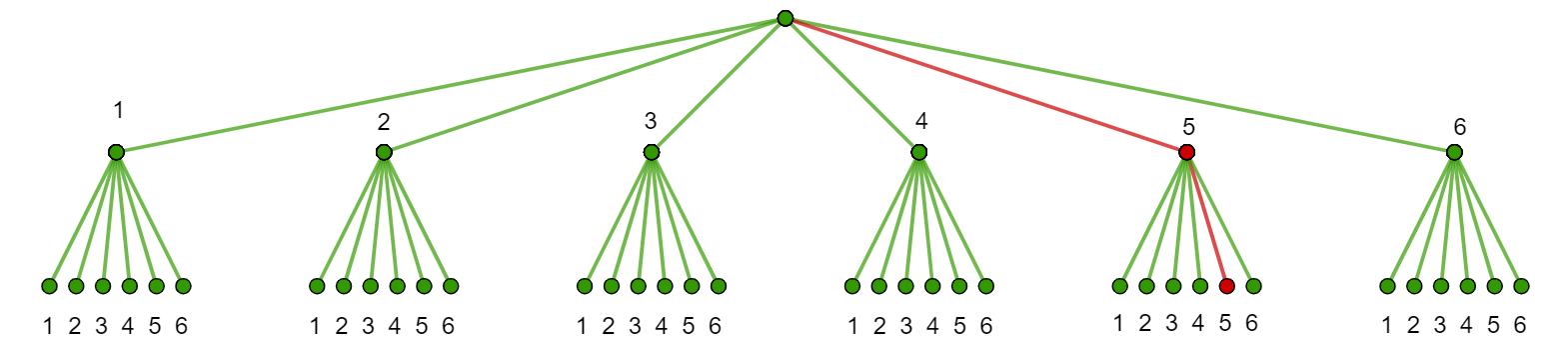
|
Enten- eller (Plus)
|
"Enten- eller princippet skal du bruge når du skal udregne sandsynligheden af flere hændelser efterfulgt af hinanden. Det vigtige er, at lægge mærke til formuleringen i opgaven. Hvis bare en af hændelserne skal være opfyldt skal du plusse sandsynlighederne sammen." Eksempel på en opgave "Du skal slå to gange med en 6-sidet terning. Udregn sandsynligheden for at du slår en 5 enten første gang eller anden gang." Det vigtige er at lægge mærke til formuleringen i opgaven. Det er lige meget om du slår en 5'er første gang eller anden gang. Derfor skal du plusse sandsynlighederne med hianden. Udregning For hver gang du slår med terningen er der 1/6 sandsynlighed for at slå en 5'er 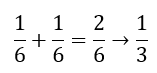
|
© 2019 All Rights Reserved. Læs om privatvilkår