Matematiksiden.dk

Deskriptorer

Observationssæt

"Et Observationssæt, også kaldet et datasæt, indholder tal som beskriver en undersøgelse. Til højre herfor er en tabel med skostørrelser i en klasse"

Herunder er et ordnet observationssæt, fordi tallene står i rækkefølge efter størrelse

36	36	38	38	39	39	39	39
39	40	40	40	41	41	42	43
43	43	44	44	45	45	46	47

Typetal

"Et typetal, er det "typiske tal" - altså det tal der forekommer flest gange i et observationssæt"

Herunder er typetallet 39, da det forekommer flest gange

36	36	38	38	39	39	39	39
39	40	40	40	41	41	42	43
43	43	44	44	45	45	46	47

Middeltal

"Middeltal, også kaldet gennemsnit, findes ved at lægge alle tallene i observationssættet sammen og dividere med antallet af observationer"

Størsteværdi

"Størsteværdi, er det største tal i observationssættet"

Herunder er størsteværdien 47, da 47 er det største tal

36	36	38	38	39	39	39	39
39	40	40	40	41	41	42	43
43	43	44	44	45	45	46	47

Mindsteværdi

"Mindsteværdi, er det mindste tal i observationssættet"

Herunder er mindsteværdien 36, da 36 er det mindste tal

36	36	38	38	39	39	39	39
39	40	40	40	41	41	42	43
43	43	44	44	45	45	46	47

Variationsbredde

"Variationsbredden, er forskellen på størsteværdien og mindsteværdien"

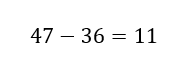
Median

"Medianen, er det midterste tal i et ordnet observationssæt"

Først skal du ordne alle tallene i observationssættet, så de står i rækkefølge
Derefter finder du det tal, der står i midten af rækkefølgen
Er der to tal i midten, lægger du de to tal sammen og dividerer med 2

36	36	38	38	39	39	39	39
39	40	40	40	41	41	42	43
43	43	44	44	45	45	46	47

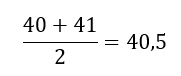
Nedre kvartil - 25%

"Nedre kvartil, også kaldet 25% kvartilen, er det tal der ligger 25% eller ¹/₄ inde i det ordnede observationssæt"
Sådan finder du nedre kvartil:

Først skal du ordne alle tal i observationssættet, så de står i rækkefølge

Derefter finder du det tal der ligger ¹/₄ eller 25% inde i observationssættet

Er der to tal der ligger 25% eller ¹/₄ inde, så lægger du de to tal sammen og dividerer med 2

Der er 24 tal i observationssættet. Derefter finder jeg ¹/₄ af 24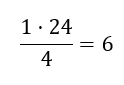

Derefter tæller jeg seks tal ind i observationssættet for at finde nedre kvartil

36 36 38 38 39 39 39 39

39 40 40 40 41 41 42 43

43 43 44 44 45 45 46 47

Nedre kvartil er derfor 39

Øvre kvartil - 75%

"Øvre kvartil, også kaldet 75% kvartilen, er det tal der ligger 75% eller ³/₄ inde i det ordnede observationssæt"
Sådan finder du øvre kvartil:

Først skal du ordne alle tal i observationssættet, så de står i rækkefølge

Derefter finder du det tal der ligger ³/₄ eller 75% inde i observationssættet

Er der to tal der ligger 75% eller ³/₄ inde, så lægger du de to tal sammen og dividerer med 2

Der er 24 tal i observationssættet. Derefter finder jeg ³/₄ af 24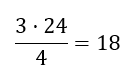

Derefter tæller jeg atten tal ind i observationssættet for at finde øvre kvartil

36 36 38 38 39 39 39 39

39 40 40 40 41 41 42 43

43 43 44 44 45 45 46 47

Øvre kvartil er derfor 43

Hyppighed

"Hyppighed, som forkortes (hx), er et tal, der beskriver hvor ofte en observation optræder i observationssættet"

"Summeret hyppighed, som forkortes (Hx), findes ved at lægge hyppighederne (hx) sammen, for hver række i tabellen"

Observationer	Hyppighed (hx)	Summeret hyppighed (Hx)
36	2	2
38	2	4
39	5	9
40	3	12
41	2	14
42	1	15
43	3	18
44	2	20
45	2	22
46	1	23
47	1	24

Det sidste tal i rækken Summeret hyppighed, skal være det samme tal som det antal observationer, der er med i undersøgelsen

Frekvens

"Frekvens, som forkortes (fx), er hvor ofte en observation optræder i observationssættet i procent"

"Summeret frekvens, som forkortes (Fx), findes ved at lægge frekvenserne (fx) sammen, for hver række i tabellen"
Udregning er frekvens, er hyppigheden for den enkelte observation, divideret med antallet af observationer, ganget med 100
Formelsamling

Observationer	Hyppighed (hx)	Frekvens (fx)	Summeret frekvens (Fx)
36	2	8,333	8,333
38	2	8,333	16,666
39	5	20	36,666
40	3	12,5	49,166
41	2	8,333	57,499
42	1	4,166	61,665
43	3	12,5	74,165
44	2	8,333	82,498
45	2	8,333	90,831
46	1	4,166	94,997
47	1	4,166	99,163
Sum af (hx)	24

Det sidste tal i rækken Summeret frekvens, skal gerne være 100 eller meget tæt på 100