Matematiksiden.dk

Grupperede observationer

Observationssæt

"Når der er mange forskellige observationer, kan det være en god ide at gruppere observationerne i nogle intervaller"

Herunder er elevernes højde i en klasse, og der er mange forskellige højder!

161	170	167	161	180	185	179	167
190	189	175	172	168	180	182	187
177	166	189	184	163	168	186	191

Gruppede observationer

"Gruppede observationer består af intervaller. Et interval starter med kantet parentes ] og slutter med en kantet parentes ].

Et interval kunne se således ud: ]165;170]. I dette interval findes alle tal fra 165 op til og med 170. Tallet 165 er IKKE med i intervallet, men alle tal fra 165

I tabellen til højre er tallet 165 med i den øverste række, men tæller ikke med i række 2 "

Grupperede observationer
]160;165]
]165;170]
]170;175]
]175;180]
]180;185]
]185;190]
]190;195]

Hyppighed

"Hyppighed er hvor mange gange en observation optræder i et interval
I tabellen til højre kan du se, at der er 3 elever i intervallet ]160;165]"

Grupperede observationer	Hyppighed (hx)
]160;165]	3
]165;170]	6
]170;175]	2
]175;180]	4
]180;185]	3
]185;190]	5
]190;195]	1

Frekvens

"Frekvens er hvor mange gange en observation optræder i et interval omregnet til procent"

Formelsamling

Grupperede observationer	Hyppighed (hx)	Frevens (fx)
]160;165]	3	12,5
]165;170]	6	25
]170;175]	2	8,333
]175;180]	4	16,667
]180;185]	3	12,5
]185;190]	5	20,833
]190;195]	1	4,166

Middeltal

"For at finde middeltallet i grupperede observationer, kræver at du følger de 3 punkter herunder:

1: Find intervalmidtpunkt
I intervallet ]165;170] er intervalmidtpunktet 167,5 da det er det midterste tal i intervallet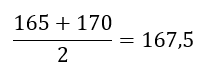

2: Gang hyppigheden med intervalmidtpunktet
Du skal lave en kolonne der hedder "Til middeltal", hvor du ganger hyppigheden med intervalmidtpunktet

3: Find middeltal
Du skal finde summen af kolonnen "Til middeltal" og dividere med antallet af observationer. I dette tilfælde er der 24 elever i klassen"

Grupperede observationer	intervalmidtpunkt	Hyppighed (hx)	Til middeltal
]160;165]	162,5	3	487,5
]165;170]	167,5	6	1005
]170;175]	172,5	2	345
]175;180]	177,5	4	710
]180;185]	182,5	3	547,5
]185;190]	187,5	5	937,5
]190;195]	192,5	1	192,5
Sum		24	4225

Udregning af middeltal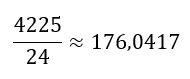

Deskriptorer

Typetal	"Typetallet, er det interval hvor der er flest observationer. Så typetallet er også et typeinterval"
Midsteværdi	"Er observationssættets mindsteværdi - alså den laveste højde i eksemplet herover"
Størsteværdi	"Er observationssættets størsteværdi - alså den højeste højde i eksemplet herover"
Variationsbredde	"Variationsbredde er forskellen på størsteværdien og mindsteværdien" Læs mere her
Median	"Median, er det midterste tal i den ordnede observation" Læs mere her
Nedre kvartil	"Nedre kvartil, er tallet der ligger ¹/₄ inde i det ordnede observationssæt" Læs mere her
Øvre kvartil	"Øvre kvartil, er tallet der ligger ³/₄ inde i det ordnede observationssæt" Læs mere her